Archimedes

dtv-Atlas zur Physik Band 1, 1987, S. 37

Prinzip des Archimedes, benannt nach ARCHIMEDES (285-212 v.Chr.): Taucht ein Körper in einen anderen ein (z. B. in eine Flüssigkeit), so wirkt auf ihn eine Auftriebskraft (Auftrieb), die der Gewichtskraft entgegengerichtet ist. Der Betrag der Auftriebskraft ist

F=mg=ρVg     Auftrieb

mit
m: die durch den eingetauchten Körper verdrängte Masse, g: örtliche Fallbeschleunigung; V eingetauchtes Volumen.

Sind beide Kräfte gleich groß, so schwimmt der Körper.

Aus der durch den Körper verdrängten Masse und der Auftriebskraft kann die Dichte eines eingetauchten Körpers bestimmt werden.

ARCHIMEDES bewies den Zeitgenossen überzeugend sein Prinzip, als er den Goldgehalt des für König Hieron Il. von Syrakus angefertigten Diadems bestimmte, ohne das Meisterstück zu beschädigen: Er tauchte den Schmuck in Wasser und bestimmte aus der verdrängten Flüssigkeitsmenge das Volumen. Wägung ergab die Masse. Er berechnete aus den beiden Meßwerten die Dichte der benutzten Legierung und verglich sie mit der von hochkarätigem Gold.

Hammer, Knauth, Kühnel: Physik 8, 1992, S.122

Aus der Geschichte der Physik

König Hieron II. von Syrakus erteilte einem Goldschmied den Auftrag, eine Krone aus purem Gold herzustellen. Das dazu nötige Gold erhielt der Goldschmied von seinem König. Obwohl dem König die künstlerische Gestaltung der Krone gefiel, plagten ihn doch Zweifel, ob die Krone wirklich aus reinem Gold bestehe. Deshalb beauftragte er Archimedes, eine Methode zu ersinnen, mit der man dies entscheiden kann, ohne die Krone zu beschädigen. Die von dem römischen Baumeister Vitruv überlieferte Legende berichtet, daß Archimedes der entscheidende Gedanke im Bad gekommen sei, nämlich als er, Archimedes, in der Badewanne untertauchte und bemerkte, daß Wasser über den Wannenrand floß. Er habe sich über seinen Einfall so gefreut, daß er, nackt und naß wie er war, durch die Straßen von Syrakus gelaufen sei, unterwegs laut heureka, heureka (ich hab's gefunden) rufend.

Bleibt die Waage, deren Balken die Königskrone und einen Körper aus reinem Gold tragen (B 45a), auch dann im Gleichgewicht, wenn man die Krone und den Körper aus Gold in Wasser bringt, so stimmen auch die beiden Auftriebskräfte und damit die Dichten überein. Enthält die Krone jedoch Silber, was tatsächlich zutraf, dann hat sie ein größeres Volumen als der Goldklumpen und erfährt eine größere Auftriebskraft (B 45b).

 B45a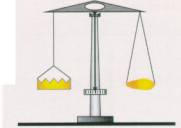B45b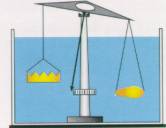

Gross Berhag: Physik, Stuttgart 1990

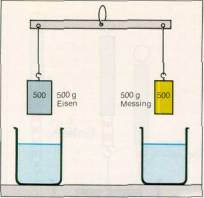
Was passiert, wenn beide Körper in Wasser getaucht werden?

Versuch des Archimedes. Um 250 v. Chr. sollte Archimedes prüfen, ob die Krone seines Königs aus reinem Gold oder nur aus einer Gold-Silber-Legierung gefertigt wurde. Dazu hängte er die Krone und einen gleich schweren Gold­klumpen an eine Balkenwaage. Dann tauchte er beide Körper in Wasser. Da nun die Waage aus dem Gleichgewicht kam, konnte er mit Hilfe des Auftriebes nachweisen, daß der Goldschmied seinen König betrogen hatte. Wir ahmen diesen Versuch nach M 54.1 nach und verwenden zwei gleich schwere Wägestücke aus Eisen bzw. Messing. Nach dem Eintauchen ins Was­ser ist das Gleichgewicht gestört: Das Eisenstück ist scheinbar leichter als das Messingstück, denn Eisen hat die kleinere Wichte, also das größere Volumen, und dazu gehört die größere Auftriebskraft.

Feuerlein/Näpfel: bsv Physik 1, München 1992

Dichte als Stoffeigenschaft. Archimedes erhielt eine interessante Aufgabe: Sein König hatte sich eine Krone anfertigen lassen. Aber dieser vermutete, daß der Goldschmied einen Teil des übergebenen Goldes durch Kupfer ersetzt hatte. Archimedes sollte, ohne die Krone zu zerstören, herausfinden, ob sie aus reinem Gold besteht. Archimedes wußte, daß „der Stoff Kupfer leichter als Gold" ist. Was bedeutet das? Eine Kupferkanne zum Beispiel ist doch schwerer als eine kleine Goldmünze. Hinter der Sprechweise „Kupfer ist leichter als Gold" verbirgt sich der Vergleich des Gewichts zweier Körper aus Kupfer und Gold von gleichem Volumen, und am gleichen Ort.

1 cm³ Kupfer ist auf der Erde schwerer als 1 cm³ Gold auf dem Mond. Das Gewicht hängt vom Ort ab. Also vergleicht man die ortsunabhängige Eigenschaft, die das Gewicht mitbestimmt, nämlich die Masse. Um herauszufinden, welche Masse 1 cm³ der Krone hat, durfte Archimedes keinen Kubikzentimeterwürfel herausschneiden. Wenn die Krone durch und durch aus dem gleichen Material besteht (homogen* ist), läßt sich die Aufgabe einfach lösen: Dividiert man die Masse m in g durch das Volumen V in cm³, ergibt sich, wieviel Gramm Material auf 1 cm³ der Krone entfallen. Man definiert deshalb die Stoff- oder materialkennzeichnende Größe ρ*:

Der Quotient aus der Masse m und dem Volumen V eines homogenen Körpers heißt Dichte ρ.              

Die Dichte ist eine abgeleitete Größe. Für ihre Einheit folgt: [ρ] = [m] :[V]. Da 1 cm³ Wasser die Masse 1 g hat, beträgt z. B. die Dichte des Wassers:

ρ_wasser =m/V = l g / 1 cm³ = 1  g/cm³

Häufig benützt man folgende vorteilhaften Zusammenstellungen von Massen- und Volumeneinheiten für [ρ]:

V Wir messen mit einer empfindlichen Balkenwaage die Masse von Würfeln der Kantenlänge 1 cm ("Einheitswürfel") aus verschiedenen Stoffen (Tab. 68.3).

Für Kupfer ergibt sich ρ_Cu = 8,9 g/cm³, für Gold ρ_Go= 19,3 g/cm³. Die Aussage „Kupfer ist leichter als Gold" muß also genauer lauten: „Kupfer hat eine kleinere Dichte als Gold".

ρ_Cu = 8,9 g/cm³ bedeutet: 1 cm³ Kupfer hat die Masse 8,9 g, n cm³ haben die Masse n • 8,9 g. Oder: Am gleichen Ort ist ein Körper aus Kupfer 8,9mal so schwer wie eine Wassermenge gleichen Volumens. Die „Dichte" ρ gibt an, wie „dicht" die Materie eines Stoffes gepackt ist.

Stoffbestimmung. Wir stellen uns eine entsprechende Aufgabe wie Archimedes:

Besteht ein uns vorliegendes rotbraunes, unregelmäßig geformtes Metallstück aus reinem Kupfer?

V Mit einer Balkenwaage bestimmen wir seine Masse zu m = 400 g.

Wie können wir das Volumen ermitteln? Archimedes fand die Lösung, als er sich in seine Badewanne setzte und dabei das Wasser anstieg.

V Tauchen wir das Metallstück in einen weiten, teilweise mit Wasser gefüllten Meßzylinder vollständig ein, können wir ablesen, um wieviel cm³ das Wasser steigt:

Diese Zunahme ist gleich dem Volumen des Metallstücks. Da die Ablesung hier nicht auf 1 cm³ genau gelingt, verbessern wir das Verfahren: Wir tauchen das Metallstück in ein Überlaufgefäß und fangen das herauslaufende Wasser auf (Abb. 69.1). Es ergibt sich V = 48 cm³ und somit p= 400 g/48 cm³ = 8,3 g/cm³ .

Aus Tab. 68.3 entnehmen wir: Das Metallstück könnte aus Messing bestehen. Messing ist eine Legierung (Mischung) aus Kupfer und Zink. Allerdings wäre ρ= 8,9 g/cm³ nur ein Indiz für Kupfer gewesen. Sicherheit brächte erst eine chemische Untersuchung. Auch Archimedes fand, daß die Dichte des Materials der Krone kleiner als die Dichte von Gold war. Die Krone bestand also nicht aus reinem Gold.

Dorn/Bader: Physik 8. Jahrgangsstufe: Hannover 1978

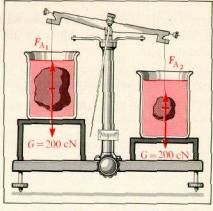
Versuch 147: An einem Waagebalken halten sich ein Messing- und ein Eisenstück von je 200 cN Gewichtskraft das Gleichgewicht (Abb. ). Taucht man beide in Wasser, so hebt sich die Seite, an der das Eisenstück hängt. Eisen (ρ = 7,9 g/cm³) verdrängt bei gleicher Gewichtskraft infolge seines größeren Volumens (25cm³) mehr Wasser, erfährt also auch einen größeren Auftrieb als Messing (ρ = 8,3 g/cm³; V = 24 cm³).

Auf diese Weise soll Archimedes nachgeprüft haben, ob ein dem König Hieron von Syrakus gelieferter goldener Kranz auch wirklich echt sei. Er tauchte den „goldenen" Kranz und einen gleich schweren Klumpen reinen Goldes an der Waage hängend in Wasser. Da sich die Seite mit dem Kranz hob, war der Goldschmied überführt, Gold zum Teil unterschlagen und durch ein gleich schweres Stück Silber ersetzt zu haben, (1 g Silber hat nach der Tabelle am Schluß des Buches ein Volumen von 1 g/ρ = 0,1 cm³, 1 g Gold von 0,05 cm³.)

Natur und Technik Physik Teilband 1: Berlin 1976

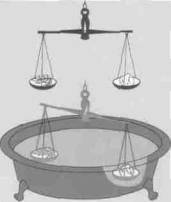 74.1: Archimedes von Syrakus (287-212 v. Chr.) war ein griechischer Mathematiker, Physiker und Konstrukteur. Die Darstellung zeigt ihn bei seinen berühmten Versuchen zum Archimedischen Prinzip.

Die Entdeckung des Archimedes

Die Gleichheit von Auftriebskraft und Gewichtskraft der verdrängten Flüssigkeit wird Archimedisches Prinzip genannt.

Die Überlieferung sagt, daß der griechische Gelehrte Archimedes (Abb. 74.1) in Syrakus die Grundlagen zur Entwicklung dieses Prinzips entdeckt habe:

König Hiero von Syrakus hatte einem Goldschmied eine bestimmte Goldmenge zur Anfertigung eines Kranzes - manche sagen, einer Krone - überlassen. Das Gewicht des Kranzes entsprach auch dem der gelieferten Goldmenge. Aufgrund der Färbung kam jedoch der Verdacht auf, ein Teil des Goldes sei unterschlagen und dafür billigeres Silber beigemischt worden. Archimedes sollte diesen Fall aufklären. Im Bade soll Archimedes dann die Lösung gefunden haben, die heute meist so dargestellt wird: Hängt man den Kranz und einen gleich schweren Goldklumpen an eine Balkenwaage und taucht beide gleichzeitig in ein Gefäß mit Wasser (Abb. 74 2), so versinkt der Goldklumpen, der Kranz aber wird angehoben. Durch die Beimischung des leichteren Silbers hat der Kranz ein größeres Volumen und damit einen größeren Auftrieb als der reine Goldklumpen gleichen Gewichts.

Durch Messen der Volumina des Kranzes und von gleich schweren Gold- und Silberklumpen im Überlaufgefäß (Abb. 74.3) konnte Archimedes die Menge des unterschlagenen Goldes feststellen.

St.-Michaels-Gymnasium Metten metten_gym@degnet.de